Definicje funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym:
Sinus kąta ostrego \alpha - (\sin \alpha) – stosunek długości przyprostokątnej leżącej naprzeciw kąta \alpha do przeciwprostokątnej.
Cosinus kąta ostrego \alpha - (\cos \alpha) – stosunek długości przyprostokątnej leżącej przy kącie \alpha do przeciwprostokątnej.
Tangens kąta ostrego \alpha - (\tg \alpha) – stosunek długości przyprostokątnej leżącej naprzeciw kąta \alpha do przyprostokątnej leżącej przy kącie \alpha .
Cotangens kąta ostrego \alpha - (\ctg \alpha) – stosunek długości przyprostokątnej leżącej przy kącie \alpha do przyprostokątnej leżącej naprzeciw kąta \alpha .
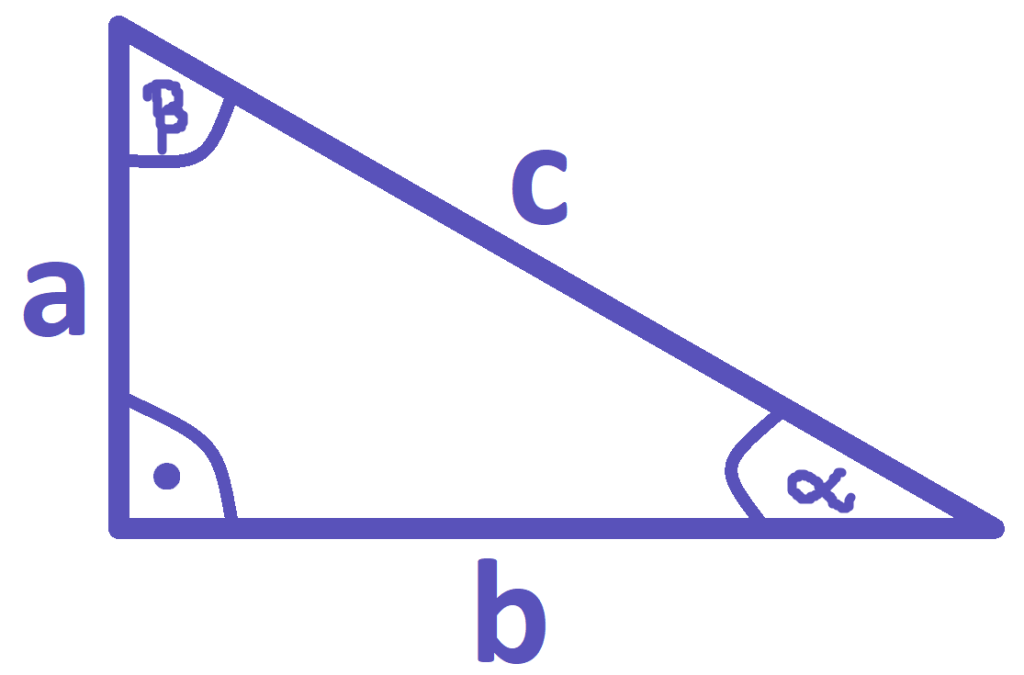
\sin \alpha = \frac{a}{c}=\cos \beta \\
\cos \alpha = \frac{b}{c}=\sin \beta \\
\tg \alpha = \frac{a}{b}=\ctg \beta \\
\ctg \alpha = \frac{b}{a}=\tg \beta \\
Tożsamości trygonometryczne
\tg \alpha = \frac{\sin \alpha}{\cos \alpha} \\
\ctg \alpha=\frac{\cos \alpha}{\sin \alpha} \\
\ctg \alpha=\frac{1}{\tg \alpha} \\
\tg \alpha=\frac{1}{\ctg \alpha} \\
\sin^2 \alpha + \cos^2 \alpha =1 – jedynka trygonometryczna
Wzory redukcyjne
\sin (90^{\circ} - \alpha)=\cos \alpha
\cos (90^{\circ} - \alpha)=\sin \alpha
\tg (90^{\circ} - \alpha)=\ctg \alpha
\ctg (90^{\circ} - \alpha)=\tg \alpha \\
\sin (90^{\circ} + \alpha)=\cos \alpha
\cos (90^{\circ} + \alpha)=-\sin \alpha
\tg (90^{\circ} + \alpha)=-\ctg \alpha
\ctg (90^{\circ} + \alpha)=-\tg \alpha \\
\sin (180^{\circ} - \alpha)=\sin \alpha
\cos (180^{\circ} - \alpha)=-\cos \alpha
\tg (180^{\circ} - \alpha)=-\tg \alpha
\ctg (180^{\circ} - \alpha)=-\ctg \alpha \\
\sin (180^{\circ} + \alpha)=-\sin \alpha
\cos (180^{\circ} + \alpha)=-\cos \alpha
\tg (180^{\circ} + \alpha)=\tg \alpha
\ctg (180^{\circ} + \alpha)=\ctg \alpha \\
\sin (270^{\circ} - \alpha)=-\cos \alpha
\cos (270^{\circ} - \alpha)=-\sin \alpha
\tg (270^{\circ} - \alpha)=\ctg \alpha
\ctg (270^{\circ} - \alpha)=\tg \alpha \\
\sin (270^{\circ} + \alpha)=-\cos \alpha
\cos (270^{\circ} + \alpha)=\sin \alpha
\tg (270^{\circ} + \alpha)=-\ctg \alpha
\ctg (270^{\circ} + \alpha)=-\tg \alpha \\
\sin (360^{\circ} - \alpha)=-\sin \alpha
\cos (360^{\circ} - \alpha)=\cos \alpha
\tg (360^{\circ} - \alpha)=-\tg \alpha
\ctg (360^{\circ} - \alpha)=-\ctg \alpha \\
\sin (360^{\circ} + \alpha)=\sin \alpha
\cos (360^{\circ} + \alpha)=\cos \alpha
\tg (360^{\circ} + \alpha)=\tg \alpha
\ctg (360^{\circ} + \alpha)=\ctg \alpha \\
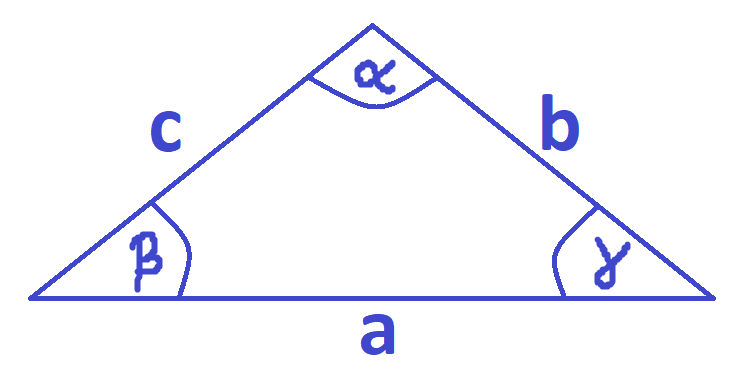
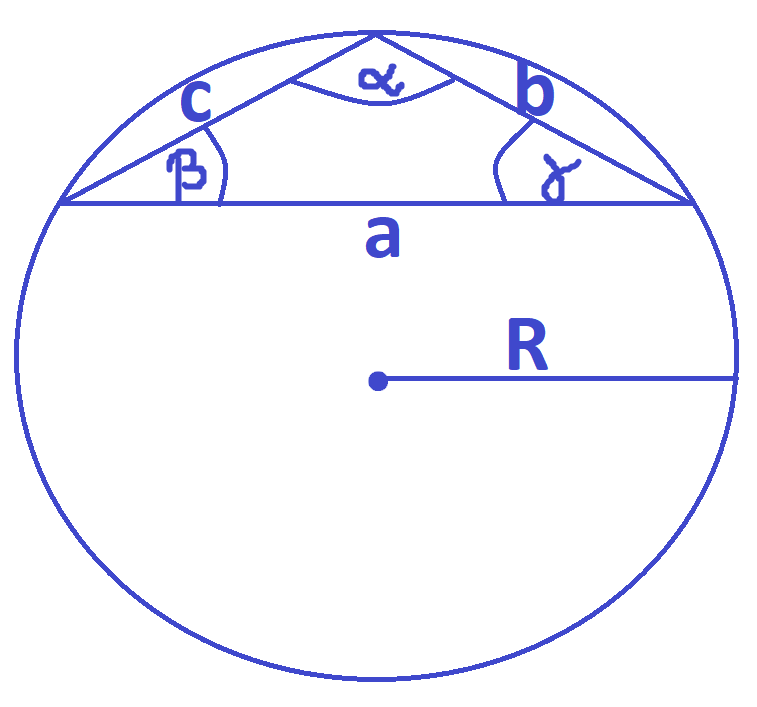
Twierdzenie sinusów
W dowolnym trójkącie stosunek długości dowolnego boku do sinusa kąta leżącego naprzeciw tego boku
jest stały i równy długości średnicy okręgu opisanego na tym trójkącie.
\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}=2R
Twierdzenie cosinusów
W dowolnym trójkącie kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków, pomniejszonej o podwojony iloczyn długości tych boków i cosinusa kąta zawartego między nimi.
Twierdzenie cosinusów często nazywane jest uogólnionym twierdzeniem Pitagorasa.
c^2=a^2+b^2-2ab\cos\gamma
b^2=a^2+c^2-2ac\cos\beta
a^2=b^2+c^2-2bc\cos\alpha